- >> Teaching / Enseignement
- >> Functional programming: Tic-Tac-Toe in CamL
Functional programming: Tic-Tac-Toe in CamL¶
We want to write a program playing Tic Tac Toe, making use of functional programming tools and trying to get rid of any imperative aspects of programming. Indeed we don’t want to have any if, then, else, ... but just functions. The player relies on the Minimax algorithm and its AlphaBeta prunning optimization. The algorithm requires to build a tree of possible game states from an initial state, trying to estimate the interest of playing each actions. An action is then taken based on these estimates.
Before solving the Tic Tac Toe game, we first introduce some functions for manipulating lists that we will be helpful for the following.
Preliminaries¶
- Write two functions first_element_couple and second_element_couple which return the first and second element of a couple.
first_element_couple : 'a * 'b -> 'a
second_element_couple : 'a * 'b -> 'b
- Write a function compose which takes two functions and returns its composition:
let h = compose f g;
(* h(x) = f(g(x)) *)
- Write a function generate_list which takes an integer n and returns the list of integers from 0 to n
generate_list 5 = [0;1;2;3;4;5]
generate_list (-1) = []
- We now write two “high level” functions which allow to easily define functions on lists. A list is a recursive structure built from the empty list and the cons operation. Our functions will replace these two elements. cons is defined as:
let cons = function a -> function l -> a::l;;
- Write two functions foldl and foldr:
foldl f z [a0;a1;a2; .... an] = f ... f (f a0 z) a1) ... an
foldr f z [a0;a1;a2; .... an] = f a0 (f a1 ( ... (f an z)...) )
- Using cons, foldr and compose, write the function map which applies a function to all the elemnts of a list:
map (function x -> 2 * x) [1;2;3] = [2;4;6]
- Using foldl and cons, write the function invert which inverts a list:
invert [1;2;3] = [3;2;1]
- Using foldr and a second function to define, write length which returns the size of a list:
length [1;2;3;4] = 4
- Using foldr and cons, write append which concatenates two lists:
append [1;2;3;4] [5;6;7] = [1;2;3;4;5;6;7]
- Making use of the max, min and foldl functions, write two functions which return the maximal and minimal value of a list. Applying these functions on empty lists will raise an error (failwith “error message”)
let max_list = function
[] -> ....
| a::l -> ...
let min_list = function
[] -> ...
| a::l -> ....
We then define the two functions max_list_with_index and min_list_width_index which allow to recover the max (or min) of a list with their indices.
let max_list_with_index = function l ->
let iter = function
[] -> failwith "An empty list has undefined max"
| a::l -> foldl
(function b -> function
(c1,c2,c3) when b > c1 -> (b,[c3],c3+1)
| (c1,c2,c3) when b = c1 -> (b,c3::c2, c3+1)
| (c1,c2,c3) -> (c1,c2, c3+1)
)
(a,[0],1) l
in let (a,b,c) = iter l in (a,b);;
let min_list_avec_index = function l ->
let iter = function
[] -> failwith "An empty list has undefined min"
| a::l -> foldl
(function b -> function
(c1,c2,c3) when b < c1 -> (b,[c3],c3+1)
| (c1,c2,c3) when b = c1 -> (b,c3::c2, c3+1)
| (c1,c2,c3) -> (c1,c2, c3+1)
)
(a,[0],1) l
in let (a,b,c) = iter l in (a,b);;
# let li = [1;8;4;8;2];;
# max_list_with_index li;;
: int * int list = (8, [3; 1])
# min_list_with_index li;;
: int * int list = (1, [0])
- Write a function draw_randomly_an_element which takes a list and returns a randomly chosen element of it and a function draw_randomly_a_position which draws a random position from a list (make use of length).
let draw_randomly_an_element = function
[] -> ...
| a::l -> foldl ....;;
let draw_randomly_a_position = function l -> ..;;
# let li = [1;8;2;3];;
# draw_randomly_an_element li;;
: int = 3
- Write a function consume_with_rest which extracts p elements from a list and returns a couple with a list of these p elements and the other unused elements.
consume_with_rest 2 [1;2;3;4;5;6] = ([1;2], [3;4;5;6])
- With the function first_element_couple and consume_with_rest, write a function consume which takes the first p elements of a list
consomme 2 [1;2;3;4;5] = [1;2]
- With the function consume_with_rest, write the function consume_spaced_with_rest which takes 3 arguments: a list l, an integer n and an integer p. It returns a list of n elements, spaced by p elements, from the list l, as well as a list of the unused elements.
consume_spaced_with_rest 2 5 [1;2;3;4;5;6] = ([1;6], [2;3;4;5])
- We then define consume_spaced as:
let consomme_espace = function n -> function p -> function l->
first_element_couple (consume_spaced_with_rest n p l);;
- We are now arriving at the two last functions for manipulating lists. Using consume_with_rest, and consume_spaced_with_rest, write the functions arange_list and arange_list_spaced that take a list l and returns a list of sub-lists of l. arange_list p l builds a list of lists, each being of p consecutive elements of l. arange_list_spaced n p l builds a list of n-length lists taken every p positions.
arange_list 3 [1;2;3;4;5;6];;
: int list list = [ [1; 2; 3]; [4; 5; 6] ]
arange_list_spaced 2 3 [1;2;3;4;5;6];;
: int list list = [ [1; 4]; [2; 5]; [3; 6] ]
The previous functions will help us to extract the rows, columns and diagonals of the Tic Tac Toe in order to determine if a position is a winning position.
- Write a function replace which replaces the i-th occurrence (positions run from 0, i.e. i=0 indicates the 1st occurrence) of an element a with element b in a list;
let rec replace = function a -> function b -> function i -> function l ->
match (i,l) with
(_,[]) ->
| (0,c::r) when c=a ->
| (_,c::r) when c=a ->
| (_,c::r) ->
replace "a" "e" 0 ["a";"b";"a"; "c"];; : string list = ["e";"b";"a";"c"]
All the above functions are provided in preliminaries.ml
Lazy Tic Tac Toe¶
To make a computer program playing Tic Tac Toe, we will make use of evaluation algorithms which quantifies the quality of each possible action (in the Tic Tac Toe game, the tree of the game is reasonably large while more probabilistic approaches are required for games as complex as the go game). In the following, we code the minimax algorithm with its alpha-beta pruning optimization. It evaluates recursively the value of a play starting from the current state of the game. The transitions between the states of a Tic Tac Toe game will be represented as a tree. In the Tic Tac Toe game, the tree has at most 9 * 8 * 7 * 6 ... = 9! nodes (a bit less however as a finished game does not have to fill the whole board and there are symmetries). Instead of representing the whole tree of the game in memory, we would like to be lazy by evaluating (and representing or unrolling) a branch of the tree only when required. This is the purpose of the lazy tree type we define below.
A Lazy tree¶
Let us define a type for our lazy tree.
type 'a tree = Leaf of 'a | LazyNode of 'a * (unit -> 'a tree) | Node of 'a * 'a tree list;;
let node = function
Leaf(m) -> m
| Node(m,_) -> m
| LazyNode(m,_) -> m;;
let rec son = function
Leaf(_) -> failwith "Trying to get the son of a leaf !!"
| Node(_,l) -> l
| LazyNode(_,f) -> son (f());;
let label_list = function l -> map node l;;
- Define the value of type int tree representing the following tree:
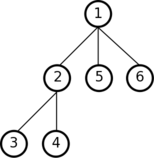
The interest of the lazy tree is exactly that it is lazy: there are branches that we will unroll on request. It can for example be used to represent infinitely deep trees.
You might test the following example:
let example_sons = function n -> [n+1; 2*n; n*n];;
let rec example_tree = function n -> LazyNode(n, function () ->
Node(n, map example_tree (example_sons n)));;
let tree_test = example_tree 3;;
sons(tree_test);;
map sons (sons tree_test);;
label_list (sons tree_test);;
The Tictactoe type¶
We now define a type for the state of a slot in the tictactoe and then the tictactoe type:
type state = Empty | X | O ;;
type tictactoe = Tictactoe of state list;;
type tictactoe_tree = tictactoe tree;;
let next_symbol = function
X -> O
| O -> X
| Empty -> failwith "Empty has no sucessor !";;
Define the values of type tictactoe for the following games:
- an initial empty board, let us call it tictactoe_empty
- a board for a game with a draw, let us call it tictactoe_draw
- a board where X is the winner, let us call it tictactoe_X
- a board where O is the winner, let us call it tictactoe_O
Displaying a board¶
- Write a function state_to_string which converts a state (X, O, Empty) into a string.
- Write a function tictactoe_to_string which converts a tictactoe (Tictactoe(t)) into a string. Each state must be converted into a string, a line break must be added at the end of each line. We can make use of the function arange_list, foldr and state_to_string.
- Defining display_tictactoe from print_string and tictactoe_to_string, we then get:
let tictactoe_to_string = function Tictactoe(t) -> ....
let display_tictactoe = function t -> print_string (tictactoe_to_string t);;
display_tictactoe tictactoe_empty;;
_ _ _
_ _ _
_ _ _
display_tictactoe tictactoe_X;;
X X X
X O O
O O X
- We now want to display a board with numbers indicating the possible moves so that a player can directly type the number of the move to play. Write a function display_tictactoe_with_choice which displays the board with different numbers in place of the empty states. You may define a local recursive function.
let display_tictactoe_with_choice = function Tictactoe(t) -> ....
display_tictactoe_with_choice tictactoe_empty;;
(0) (1) (2)
(3) (4) (5)
(6) (7) (8)
display_tictactoe_with_choice tictactoe_X;;
X X X
O O (0)
(1) (2) (3)
Testing the end of game¶
- We are now stepping toward writting a function to determine if the game is finished, if there is a winner or if it is a draw. Write three functions extract_lines, extract_columns and extract_diagonals for extracting the lines, columns and diagonals as a state list list.
extract_lines(tictactoe_X);;
- : state list list = [[X; X; X]; [O; O; Empty]; [Empty; Empty; Empty]]
extract_columns(tictactoe_X);;
- : state list list = [[X; O; Empty]; [X; O; Empty]; [X; Empty; Empty]]
extract_diagonals(tictactoe_X);;
- : state list list = [[X; O; Empty]; [X; O; Empty]]
- Write a function is_winning_board which takes a TicTacToe and a symbol (X or O) and returns a boolean telling whether the board is won by the symbol or not.
is_winning_board tictactoe_X X;;
- : bool = true
is_winning_board tictactoe_X O;;
- : bool = false
is_winning_board tictactoe_O X;;
- : bool = false
is_winning_board tictactoe_O O;;
- : bool = true
is_winning_board tictactoe_empty X;;
- : bool = false
is_winning_board tictactoe_empty O;;
- : bool = false
- Write a function number_remaining_plays which returns the number of remaining plays (i.e. Empty slots). Write a function is_draw_board which tests if the board is a draw, meaning there is no more Empty slots and none of the players won the game. You can then write the function end_of_game which returns a boolean indicating if the game is finished.
end_of_game(tictactoe_empty);;
- : bool = false
end_of_game(tictactoe_X);;
- : bool = true
end_of_game(tictactoe_O);;
- : bool = true
end_of_game(tictactoe_draw);
- : bool = true
Gametree¶
We now turn to writing functions for constructing the gametree.
- Using replace, write a function next_board which takes a board, a symbol (X or O) and the number of a move (starting from 0) and returns the next board with the move being played. Write also a function next_possible_boards which returns a list of the next possible boards given a current board and a symbol (X or O).
next_possible_boards tictactoe_empty X;;
[Tictactoe [X; Empty; Empty; Empty; Empty; Empty; Empty; Empty; Empty];
Tictactoe [Empty; X; Empty; Empty; Empty; Empty; Empty; Empty; Empty];
....
Tictactoe [Empty; Empty; Empty; Empty; Empty; Empty; Empty; Empty; X]]
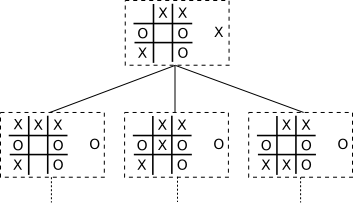
- We can now write the function gametree which takes the symbol to play and a current board and returns a LazyTree. If the board is final, we build a Leaf otherwise it is a node with lazynodes as son. Each node of leaf is labelled with the symbol of the player who plays and the current state of the board, i.e. we build a (state * tictactoe) tree.
let rec gametree = function symbol -> function board -> ...
gametree X tictactoe_test;;
- : (state * tictactoe) tree =
Node ((X, Tictactoe [Empty; X; X; O; Empty; O; X; Empty; O]),
[LazyNode ((O, Tictactoe [X; X; X; O; Empty; O; X; Empty; O]), <fun>);
LazyNode ((O, Tictactoe [Empty; X; X; O; X; O; X; Empty; O]), <fun>);
LazyNode ((O, Tictactoe [Empty; X; X; O; Empty; O; X; X; O]), <fun>)])
We have therefore built a lazytree which hosts couples with the current board and the symbol of the next move. The above tree looks like below:
Evaluating a gametree¶
- We first write a function to statically evaluate a position. Given a symbol and a board, we give a score of +1 if the board is won by the symbol, -1 if the board is won by the other player and 0 otherwise. This is a very poor heuristic and later on we will see more advanced ways to evaluate a position (minimax and alpha-beta); Write such a static_evaluation function.
let static_evaluation = function symb -> function board -> ...
static_evaluation X tictactoe_X;;
- : float = 1.
static_evaluation O tictactoe_X;;
- : float = -1.
static_evaluation X tictactoe_O;;
- : float = -1.
static_evaluation O tictactoe_O;;
- : float = 1.
static_evaluation X tictactoe_draw;;
- : float = 0
static_evaluation O tictactoe_draw;;
- : float = 0
- We now want to evaluate a board making use of the minimax algorithm. When two players play the tictactoe, they have opposite goals: they both want to win. The minimax simply states that the score of a position is the maximum value of the scores of the boards we reach if I’m the one who plays and the minimal value of the score of the boards we reach if it is the turn of the opponent. Therefore, evaluating a position is about alternating max and min from the leafs up to the current board. We want to write a function minimax which takes the symbol of the next player to play and the current board and returns a tree with a single leaf if the game is over, the label of which being the score of the board for this player, or a Node with as many Leafs sons as there are moves to play. Again, the labels of the nodes and leafs are the scores of the boards. A possible implementation and test might be:
let minimax = function symbol -> function board ->
let rec iter = function
Leaf(c) -> ...
| Node(c,l) when (first_element_couple c) = symbol -> ...
| Node(_,l) -> ...
| LazyNode(c, f) -> ...
and board_tree = gametree symbol board
in match board_tree with
Leaf(c) -> Leaf(static_evaluation symbol (second_element_couple c))
| Node(_,l) -> let lmax = map iter l in Node(max_list lmax, map (function a -> Leaf a) lmax)
| LazyNode(_,_) -> failwith "This will never happen";;
display_tictactoe tictactoe_test;;
_ X X
O _ O
X _ O
minimax O tictactoe_test;;
- : float tree = Node (1., [Leaf (-1.); Leaf 1.; Leaf (-1.)])
(* The following will be very very long *)
minimax O tictactoe_empty;;
Unfortunately, this is far too long for the very first moves as the algorithm completly unfolds all the possible games. In memory, this is not a big issue as we unfold on request but in time... A significant speed-up can be obtained making use of AlphaBeta prunning. Indeed, from the current board, if you already know that one of the next positions is a winning position, you don’t need to evaluate the other possibilities, you already known which move to play. If the current node is the play of the opponent if you already know that one of the sons is winning for him, then you know the value of the current node as well. These are the alpha and beta cuts. To write the minimax with alpha-beta prunning, you can take the same code as the minimax above and the modify the filtering of the recursive iter functions with the Node(_,_) value. In these functions, you might have used the max_list and min_list recursive functions. Now, you just need to manually unroll these recursive functions to decide whether you stop or go on evaluating the sons. This might give you something like the following:
let minimax_alphabeta = function symbol -> function board ->
let rec iter_min_sons = function current_min -> function l -> match (current_min, l) with
(-1.0, _) -> ...
| (_, []) -> ....
| (_, t::q) -> ...
and iter_max_sons = function current_max -> function l -> match (current_max, l) with
(1.0, _) -> ...
| (_, []) -> ...
| (_, t::q) -> ...
and iter = function
Leaf(c) -> static_evaluation symbol (second_element_couple c)
| Node(c,l) when (first_element_couple c) = symbol -> iter_max_sons (-1.0) l
| Node(_,l) -> iter_min_sons 1.0 l
| LazyNode(c, f) -> iter (f())
and board_tree = gametree symbol board
in match board_tree with
Leaf(c) -> Leaf(static_evaluation symbol (second_element_couple c))
| Node(_,l) -> let lmax = map iter l in Node(max_list lmax, map (function a -> Leaf a) lmax)
| LazyNode(_,_) -> failwith "This will never happen";;
Measuring the execution time of minimax and minimax_alphabeta, you might get something like:
time minimax_alphabeta O tictactoe_empty;;
- Execution time: 8.912000 s.
time minimax O tictactoe_empty;;
- Execution time: 49.652000 s.
You can now embed everything in a function to select an action and play the game. The full solution is given in preliminaries.ml and tictactoe.ml.