POMDP in a Maze¶

Problem¶

An agent is dropped somewhere, at an unknown location of a Maze. The agent has the map of the maze and a compass. He can see if there are walls all around him (west, north, east, south). Unfortunately, he has unreliable sensors, his lamp is flashing; sometimes he sees a wall while there is no, and sometimes he sees no wall while there is one. How an agent can determine where he is ? (then reaching the exit is much easier). We will consider two situations. In the first one, he is just making random actions and tries to locate himself. In the second one, we will try to set up a less naive policy to help the agent finding its location in the maze.

Formalization¶

One way to solve this problem is to make use of the formalization of Partially Observable Markovian Decision Processes within the framework Reinforcement Learning.

A POMDP is defined as a tuple (S, A, O, P, R) where:

• \(S\) is a finite set of states (where the agent can be)
• \(A\) is a finite set of actions (go straight, go left, go right)
• \(T : S \times A \times S \rightarrow [0,1]\) is a probabilistic transition function (in our case, it will be deterministic)
• \(\Omega\) is a finite set of observations (I see a wall in front of me)
• \(O : S \times \Omega \rightarrow [0,1]\) is a probabilistic observation function
• \(R\) is a reward function

At each time, the agent is in a state s, performs action a and arrives in state s’ with a probability T(s’/ s, a). As the agent is walking on ice, this really is a probability as the agent may stay at the same location even if it is trying to move. As the sensors are unreliable, it is sensing its environment from state \(s\) and observes \(w \in \Omega\) with a probability \(O(s, w)\). To be more specific with respect to our problem, \(S = \{(i,j), i \in [0, H-1], j \in [0, W-1]\}\) for a maze of width W and height H. A is simply the set \(\{0, 1, 2, 3\}\) for going west, north, east and south. \(\Omega\) contains all the 16 possible observations represented as boolean tuples of length 4 indicating with False for a wall, and true otherwise for (west, north, east, south). Then we need to compute the \(O(s,w)\) and \(T(s,a,s')\) functions. Given the observations, states and actions are discrete and finite, these are just matrices. The transition function is deterministic and will be very sparse.

Estimating the location from random moves¶

In order to represent the probability of being in state \(s \in S\), we introduce the so-called belief state \(b : S \rightarrow [0, 1]\). This is a probabiltiy distribution over the states, i.e. \(\sum_{s \in S} b(s) = 1\) (the agent is definitely in the maze!). We want to update the belief state after each action and we hope that the belief state will converge to a peaky distribution where the agent truly is. Hopefully, this might be reached in a finite number of actions.

We start with an initial belief \(b_0\), say uniform over the states the agent can possibly occupy in the maze. At step \(k\), the agent, having a belief \(b_k\), performs action \(a_k=a \in A\) and observes \(o_k=o \in \Omega\). What is \(b_{k+1}\), i.e. which are now the probabilities of occupying each of the states \(s' \in S\)?

In this update of the belief state, we get the known observation and transition functions as well as the previous belief state. Iterating few times the agent can localize himself in the maze. Below we show some examples of the belief state as the agent has moved in the maze. The illustrations have been generated with the python script maze_random_position.py. Some mazes to use with the script maze1.pnm, maze2.pnm, maze3.pnm, maze4.ppm. Click on the illustrations to get larger versions.

Initial	Middle	End

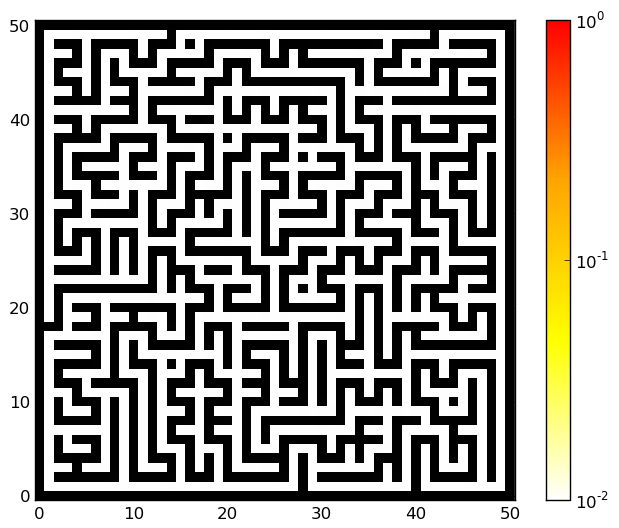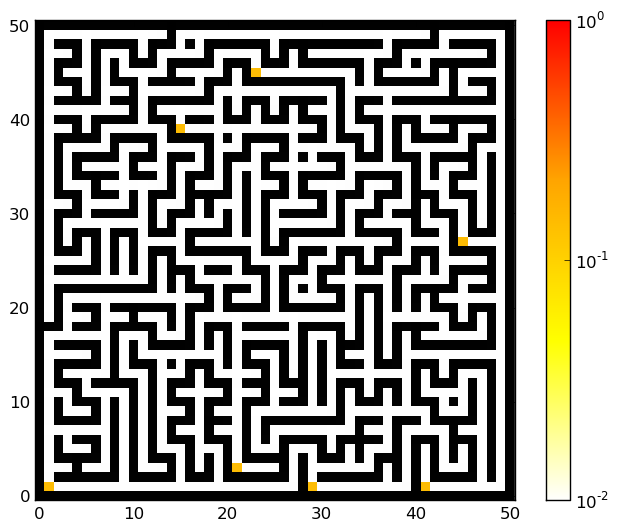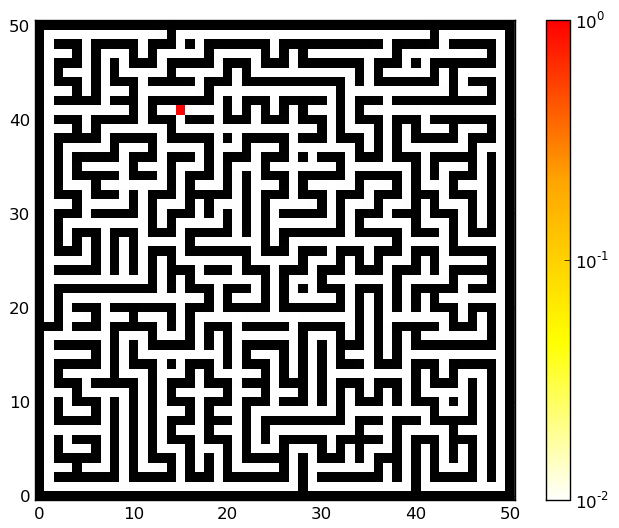Sampling the environment optimally¶

In order to determine which move to make we compute the variance of the random observation and take the action which leads to the highest variance.

to come